Apply laws of exponents to write an equivalent expression – Buckle up for an electrifying ride as we delve into the captivating world of exponents! This comprehensive guide will equip you with the power to apply the laws of exponents like a pro, enabling you to conquer any mathematical challenge that comes your way.
Mastering the laws of exponents empowers you to transform complex expressions into their equivalent forms. If you’re feeling crossword-savvy, test your skills with all for an anthem writer crossword . Then, return to the realm of exponents and conquer the challenge of rewriting expressions with precision and finesse.
Get ready to simplify expressions, expand them with ease, and master the art of working with rational exponents. Along the way, we’ll uncover the practical applications of exponents in various branches of mathematics, leaving you in awe of their versatility.
Applying the laws of exponents is a breeze when you’re looking to simplify complex expressions. It’s like when a company has an ecommerce checkout workflow that writes flawless code. You can use these laws to rewrite the expression in an equivalent form, making it easier to solve.
Just remember to keep those exponents in check!
Laws of Exponents
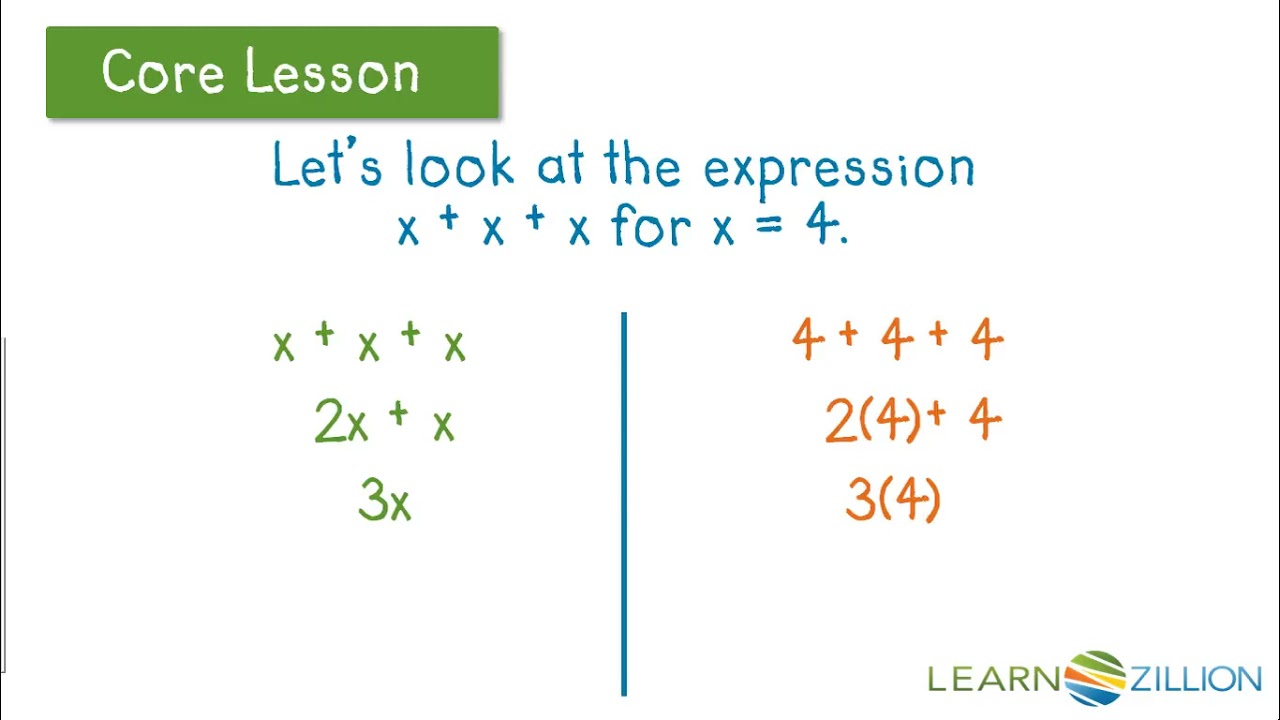
The laws of exponents are a set of rules that allow us to simplify and expand mathematical expressions involving exponents. Exponents are numbers that indicate how many times a base number is multiplied by itself. For example, 2 3means 2 multiplied by itself 3 times, which equals 8.
Applying the laws of exponents is a piece of cake when you’ve got the right tools. And speaking of tools, have you heard about an app to write a book ? It’s like a magic wand for authors, making the writing process a breeze.
But back to our exponents, these laws are like superpowers that let you simplify and transform expressions with ease.
The laws of exponents are:
- Product Rule:a m– a n= a m+n
- Power Rule:(a m) n= a m*n
- Quotient Rule:a m/ a n= a m-n
- Zero Exponent Rule:a 0= 1
- Negative Exponent Rule:a -n= 1/a n
These rules can be used to simplify expressions like:
- 2 3– 2 5= 2 3+5= 2 8= 256
- (3 2) 4= 3 2*4= 3 8= 6561
- 10 6/ 10 3= 10 6-3= 10 3= 1000
Simplifying Expressions
The laws of exponents can also be used to simplify expressions with negative exponents. For example:
- 2 -3= 1/2 3= 1/8
- (3 -2) 4= 3 -2*4= 3 -8= 1/3 8= 1/6561
- 10 -6/ 10 3= 10 -6-3= 10 -9= 1/10 9= 0.000000001
Expanding Expressions, Apply laws of exponents to write an equivalent expression
The laws of exponents can also be used to expand expressions. For example:
- (2x 3)(3x 5) = 6x 3+5= 6x 8
- (x 2+ y 3) 4= x 2*4+ 4x 2y 3+ 6x 2y 6+ 4xy 9+ y 3*4
Rational Exponents
Rational exponents are exponents that are fractions. For example, 2 1/2is the square root of 2. Rational exponents can be simplified using the laws of exponents.
An effective introduction states the writer’s purpose and provides a roadmap for the rest of the paper . In the same vein, when applying the laws of exponents to write an equivalent expression, it’s crucial to clearly state the goal and provide a step-by-step process to achieve it, ensuring a well-structured and comprehensible solution.
- a 1/n= √(a)
- a m/n= (a 1/n) m= √(a m)
For example:
- 2 1/2= √(2) ≈ 1.414
- 3 2/3= (3 1/3) 2= √(3) 2≈ 1.732
Applications in Mathematics
The laws of exponents are used in many different areas of mathematics, including algebra, geometry, and calculus. For example, the laws of exponents are used to solve equations, simplify expressions, and find derivatives.
Applying the laws of exponents to write an equivalent expression can be as easy as using an app you can write on pictures . With a few simple steps, you can simplify complex expressions and solve equations like a pro.
The key is to understand the rules of exponents and how they apply to different operations.
The laws of exponents are an essential tool for anyone who wants to understand mathematics. By understanding these laws, you will be able to simplify and expand expressions, solve equations, and find derivatives.
Final Wrap-Up
So, whether you’re a math whiz or just starting your journey, this guide is your ultimate companion. Embrace the power of exponents, and let’s embark on an unforgettable mathematical adventure together!
Expert Answers: Apply Laws Of Exponents To Write An Equivalent Expression
What are exponents?
Applying the laws of exponents to write an equivalent expression is a skill that comes in handy in various situations. Like that time you wanted to annotate your favorite meme but couldn’t find an app that lets you write on pictures ? It’s like a superpower for math enthusiasts, enabling them to simplify complex expressions with ease.
But fear not, for this skill is not limited to the realm of academia; it can empower you in the digital world too!
Exponents are mathematical symbols that represent repeated multiplication. For example, 2^3 means 2 multiplied by itself three times (2 x 2 x 2).
How do I simplify expressions with exponents?
To simplify expressions with exponents, you can use the product rule (a^m x a^n = a^(m+n)), the power rule ((a^m)^n = a^(m x n)), and the quotient rule (a^m / a^n = a^(m-n)).
What are rational exponents?
Rational exponents are exponents that are fractions. For example, 2^(1/2) is the square root of 2.
When you apply the laws of exponents to write an equivalent expression, you’re basically using the rules of algebra to simplify a complex expression. It’s like when a writer uses language in an argumentative essay to make their point clearer and more persuasive.
a writer should use language in an argumentative essay. By understanding the laws of exponents, you can simplify expressions and make them easier to work with, just like a writer can use language to make their arguments more effective.