Associative law of addition to write an equivalent expression – The associative law of addition empowers us to rearrange the grouping of numbers when adding, without altering the result. It’s a game-changer for simplifying calculations and unlocking algebraic solutions.
The associative law of addition allows you to rearrange addends in an expression without changing its value. For example, 3 + 4 + 5 is equivalent to 4 + 5 + 3. This property is useful in many situations, such as when an insurance company writes a policy to the effect that the insured is covered for a certain amount of money in the event of an accident.
The insurance company may use the associative law of addition to calculate the total amount of coverage by adding the amounts of coverage for each type of accident.
This mathematical superpower lets us swap the order of terms, like magic, while maintaining the same outcome. Get ready to dive into the world of equivalent expressions and discover the transformative power of the associative law of addition.
Yo, check it, the associative law of addition lets you rearrange numbers to make equal expressions. Like, you can switch up the order of the addends and it’ll still equal the same. For example, 2 + 3 + 4 = 4 + 2 + 3. It’s like when you’re writing an apology letter using an ai write an apology letter . You can rearrange the words and it’ll still mean the same thing, like “I’m sorry” or “Apologies for my mistake.”
Associative Law of Addition
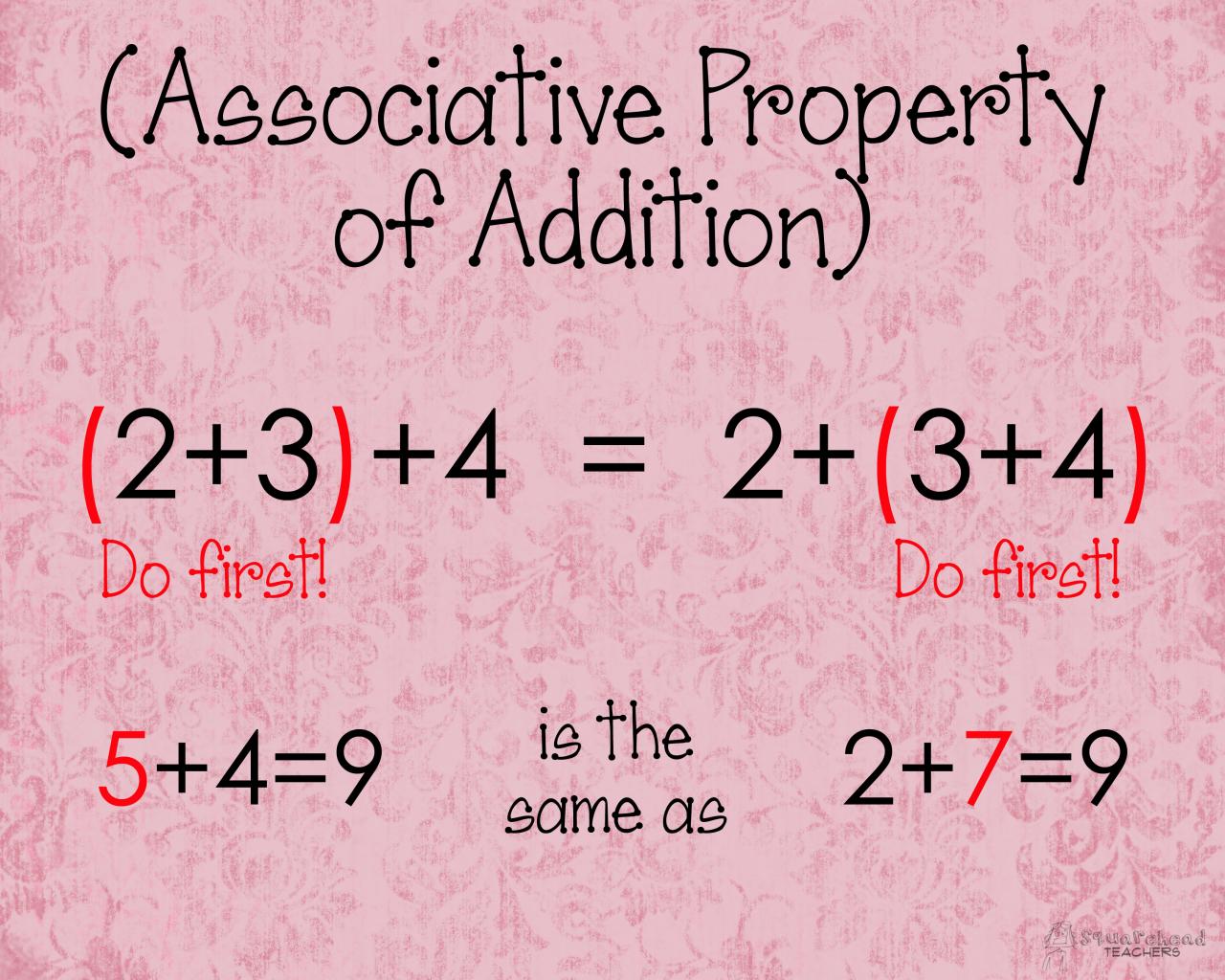
The associative law of addition states that when adding three or more numbers, the grouping of the numbers does not affect the sum. In other words, you can add the numbers in any order and get the same result.
Associative law of addition lets you write an equivalent expression by grouping terms differently. Like, when you have a headache, an an error occurred while launching this game disk write error can be a bummer. But don’t worry, you can still apply the associative law to regroup the aspirin, ibuprofen, and caffeine to find relief.
Mathematical Representation
The associative law of addition is represented mathematically as follows:
(a + b) + c = a + (b + c)
Using the associative law of addition, you can rearrange numbers in an expression to create an equivalent one. This concept applies not only to math but also to the workplace. For instance, when writing up an employee, a write up for an employee , you can organize the information in various ways while still conveying the same message.
Similarly, in math, the order of numbers in an addition expression doesn’t alter the sum.
Equivalent Expression
Using the associative law of addition, you can rearrange the terms in an expression to create an equivalent expression. For example:
(5 + 3) + 2 = 5 + (3 + 2)
In mathematics, the associative law of addition states that the grouping of addends does not affect the sum. For example, (a + b) + c = a + (b + c). This law allows us to write equivalent expressions, such as 3 + 4 + 5 = 3 + (4 + 5) = 12. Similarly, if you’ve ever used an AI assistant to write an apology, like ai write me an apology , you’ll know that it can be helpful to rearrange the order of the words to create a more concise and effective message.
The associative law of addition can also be used to simplify expressions with multiple addends.
Both expressions evaluate to 10.
The associative law of addition states that you can group numbers in any order when adding them. For example, (2 + 3) + 4 = 2 + (3 + 4). This property is useful for simplifying expressions and solving equations.
Becoming an English teacher requires a strong understanding of grammar and syntax. However, the associative law of addition can also be used to simplify sentences and make them easier to understand.
Examples and Applications
The associative law of addition is used in many real-world applications, such as:
- Simplifying mathematical calculations
- Solving algebraic equations
- Calculating averages and sums
Applications in Algebra, Associative law of addition to write an equivalent expression
The associative law of addition is essential in algebra. It allows us to simplify and solve algebraic expressions by grouping terms and rearranging them.
Associative law of addition allows us to rearrange addends without changing the sum, just like a person who writes slogans for an advertisement can rearrange words to create different messages. With this law, we can write equivalent expressions that make calculations easier.
Applications in Real-World Scenarios
The associative law of addition is used in various fields, including:
- Finance: Calculating interest and payments
- Physics: Adding forces and velocities
- Engineering: Designing structures and systems
End of Discussion: Associative Law Of Addition To Write An Equivalent Expression
The associative law of addition is not just a mathematical rule; it’s a tool that unlocks the potential for simpler calculations, efficient problem-solving, and a deeper understanding of algebra. Embrace its power and witness the transformation in your mathematical journey.
FAQ Section
What’s the associative law of addition?
It’s a mathematical rule that states the order in which you add numbers doesn’t affect the result.
How can I use it to find equivalent expressions?
Rearrange the terms within the parentheses or brackets without changing the order of operations.
Where is the associative law of addition used in real life?
It’s used in accounting, finance, and even everyday calculations like splitting a bill or figuring out the total cost of groceries.