For each of the number line write an absolute value – In the realm of mathematics, absolute values hold a pivotal role, providing a means to quantify the magnitude of numbers, regardless of their sign. Join us as we embark on a journey through the fascinating world of absolute values, exploring their definition, properties, and myriad applications.
From the depths of number lines to the complexities of equations, we will unravel the mysteries of absolute values, empowering you with a profound understanding of this essential mathematical concept.
1. Definition of Absolute Value
In mathematics, the absolute value of a number is its distance from zero on the number line. It is represented by two vertical bars around the number, like this: |x|. The absolute value of a positive number is the number itself, and the absolute value of a negative number is the opposite of the number.
For example, the absolute value of 5 is 5, and the absolute value of -5 is also 5. This is because 5 and -5 are the same distance from zero on the number line.
The absolute value of a number has several important properties. First, the absolute value of a number is always positive or zero. Second, the absolute value of a product of two numbers is equal to the product of the absolute values of the two numbers.
Third, the absolute value of a quotient of two numbers is equal to the quotient of the absolute values of the two numbers.
Examples, For each of the number line write an absolute value
- |5| = 5
- |-5| = 5
- |-10| = 10
- |0| = 0
- |x| = x, if x ≥ 0
- |x| = -x, if x< 0
Properties
- |a| ≥ 0 for all real numbers a
- |ab| = |a||b| for all real numbers a and b
- | | = |a/b| for all real numbers a and b, where b ≠ 0
2. Absolute Value on a Number Line
The number line is a straight line that represents all the real numbers. The positive numbers are to the right of zero, and the negative numbers are to the left of zero.
The absolute value of a number is its distance from zero on the number line. For example, the absolute value of 5 is 5, and the absolute value of -5 is also 5. This is because 5 and -5 are the same distance from zero on the number line.
The absolute value of a number can be used to find the distance between two points on the number line. For example, the distance between 5 and -5 is 10, because the absolute value of 5 – (-5) is 10.
Distance Between Points
The distance between two points on a number line is the absolute value of the difference between the two points. For example, the distance between 5 and -5 is 10, because the absolute value of 5 – (-5) is 10.
Applications
- Finding the distance between two points on a map
- Measuring the error in a measurement
- Calculating the magnitude of a vector
3. Applications of Absolute Value: For Each Of The Number Line Write An Absolute Value
Absolute values have a wide range of applications in mathematics, science, and engineering. Here are a few examples:
- In physics, absolute values are used to measure the magnitude of vectors. A vector is a quantity that has both magnitude and direction. The magnitude of a vector is its length, and it is always positive.
- In economics, absolute values are used to measure the size of errors. For example, the absolute value of the difference between the actual value of a good and the predicted value of a good is called the error.
- In engineering, absolute values are used to calculate the distance between two points. For example, the absolute value of the difference between the x-coordinates of two points is the distance between the two points in the x-direction.
4. Absolute Value Inequalities
An absolute value inequality is an inequality that involves the absolute value of a variable. For example, the inequality |x| > 5 means that the distance between x and 0 is greater than 5.
Absolute value inequalities can be solved using the following steps:
- Isolate the absolute value expression on one side of the inequality.
- Split the inequality into two cases: one case where the expression inside the absolute value is positive, and one case where the expression inside the absolute value is negative.
- Solve each case separately.
- Combine the solutions from both cases.
Examples, For each of the number line write an absolute value
- Solve the inequality |x| > 5.
- Solve the inequality |x – 3| ≤ 2.
- Solve the inequality |2x + 1| > 4.
5. Absolute Value Equations
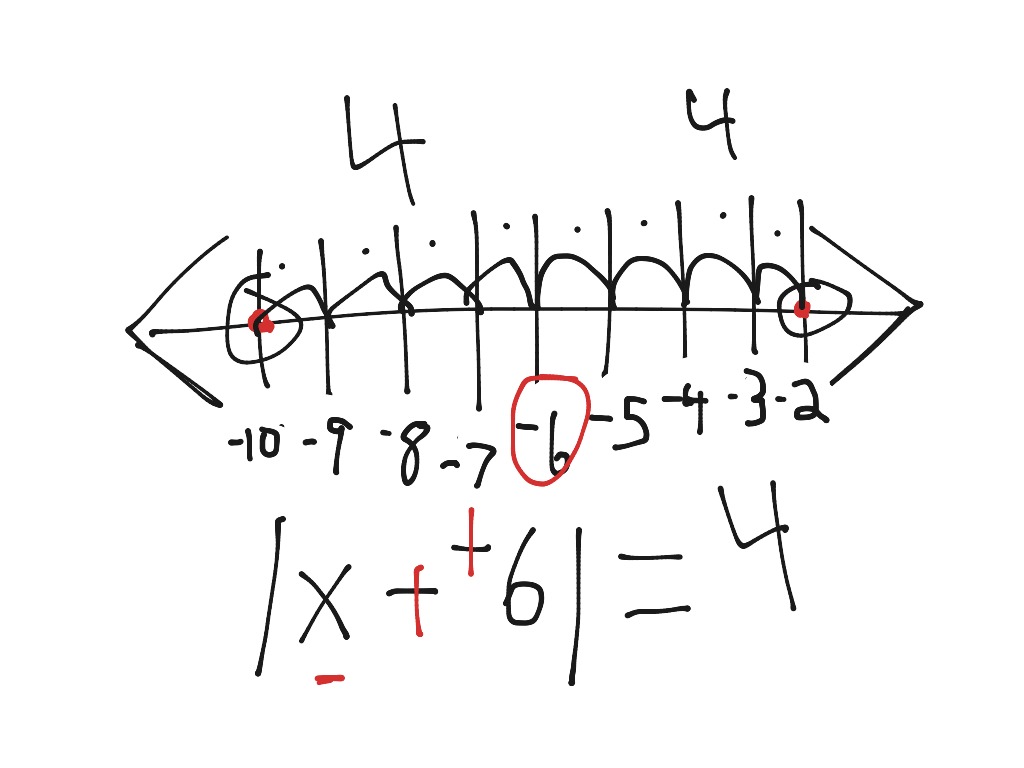
An absolute value equation is an equation that involves the absolute value of a variable. For example, the equation |x| = 5 means that the distance between x and 0 is 5.
Absolute value equations can be solved using the following steps:
- Isolate the absolute value expression on one side of the equation.
- Split the equation into two cases: one case where the expression inside the absolute value is positive, and one case where the expression inside the absolute value is negative.
- Solve each case separately.
- Combine the solutions from both cases.
Examples, For each of the number line write an absolute value
- Solve the equation |x| = 5.
- Solve the equation |x – 3| = 2.
- Solve the equation |2x + 1| = 4.
6. Properties of Absolute Value
The absolute value function has a number of important properties. These properties can be used to simplify absolute value expressions and to solve absolute value equations and inequalities.
- Triangle Inequality: For any two real numbers a and b, |a + b| ≤ |a| + |b|.
- Multiplication Property: For any real number a and any positive number b, |ab| = |a||b|.
- Division Property: For any two real numbers a and b, where b ≠ 0, |a/b| = |a|/|b|.
Examples, For each of the number line write an absolute value
- Use the triangle inequality to simplify the expression |5 + 3|.
- Use the multiplication property to simplify the expression |2x – 3|.
- Use the division property to simplify the expression |10/5|.
Conclusion
Our exploration of absolute values culminates in a comprehensive understanding of their significance in mathematics. Whether grappling with distances on a number line, solving equations, or navigating the intricacies of inequalities, absolute values serve as an indispensable tool. Their properties, such as the triangle inequality and the multiplication property, provide a solid foundation for solving complex mathematical problems.
With this newfound knowledge, you are now equipped to conquer any mathematical challenge involving absolute values, unlocking a world of possibilities in your mathematical endeavors.
Detailed FAQs
What is the absolute value of a number?
The absolute value of a number is its distance from zero on the number line. It is always positive or zero.
How do you find the absolute value of a number?
To find the absolute value of a number, simply remove its sign (if it has one) and write the resulting number.
What are the properties of absolute values?
Absolute values have several important properties, including the triangle inequality, the multiplication property, and the division property.